[알고리즘] 0-1 knapsack
- [ CS기초 ]/알고리즘
- 2022. 9. 12.
예전에 풀고 정리했었는데 까먹어서 다시 정리해봄. 분명히 이해하고 넘어갔는데 왜 지금 보니깐 이해가 안되지??
BOJ 12865) 평범한 배낭

물건을 쪼개어 가져갈 수 있는 fraction knapsack문제에서는 무게당 가치(v/w)가 높은 순으로 가져가면 된다. 하지만 위와 같은 0-1 knapsack 문제는 greedy한 방법으로는 풀 수 없다.
for(int i = 1; i <= N; i++) { //N개의 물건
for(int j = 1; j <= K; j++) { //가능한 최대 무게
if(j >= w[i])
dp[i][j] = Math.max(v[i] + dp[i-1][j - w[i]], dp[i-1][j]); //이번물건 넣는경우 + 안넣는경우
else
dp[i][j] = dp[i-1][j];
max = Math.max(dp[i][j], max);
}
}
dp[i][j]에서 i는 현재 넣은 물건의 번호, j는 가방의 최대 무게제한을 의미하고, dp[i][j]의 값은 가치를 나타낸다. 즉 dp[5][60]은 5번 물건까지 고려하고 가방의 무게제한이 60일때 배낭의 최대 가치를 말한다,
그런데 도대체 왜 이런식으로 dp 배열을 구성할까? 문제의 포인트는 가능한 최대 무게를 찾는 것이기에, i번째 물건까지 넣을 수 있을 때, 가능한 최대 무게 j에서 가질 수 있는 최대 가치가 무엇일까를 찾는 식으로 dp를 수행하는 것이다.

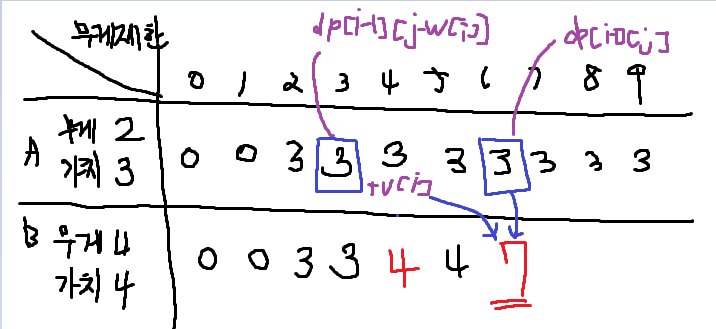
이해를 돕기 위해, 가장 먼저 i가 1일때를 생각해보자. 가장 먼저 고려할 물건은 무게가 2이고 가치가 3인 물건 A이다. 무게 제한이 2가 되기 이전에는 A를 넣을 수 없으므로 가치가 0이고, 제한이 2가 되면 A를 추가할 수 있으므로 이후로는 배낭의 최대 가치가 3이 된다.

이번에는 i가 2일때를 생각하자. 이 경우 두번째 물건인 B까지도 고려한다. 그런데 이 경우 i가 1이었던 방금 상황과는 조금 다름을 알 수 있다. B의 무게는 4이므로, 무게제한이 4가 되기 이전에는 B를 최대 가치에 포함시킬 수 없음에도, 물건 A를 고려하면 물건 A의 가치를 고려해주어야 한다. 조금 더 생각해보면, 현재 물건 i를 포함시킬 수 없을 경우에는 물건 i-1까지만을 고려한 가치값이 그대로 넘어오는 것을 알 수 있다. 따라서 다음과 같은 점화식이 나온다.
if(가방이 비어있고, 물건 i가 가방에 들어갈 수 있을 때)
dp[i][j] = dp[i-1][j];

그렇게 무게제한을 증가시키면서 케이스를 고려하다 보면, 현재 물건 B의 무게가 전체 무게제한과 같아져서 물건을 포함시킬 수 있는 경우가 나온다. 이때는 이미 구해놓은, A까지만 고려했을때의 최대 가치와 B를 첨가했을때의 무게 가치를 비교하여 더 큰값을 고르면 된다.

그런데 위와 같이 단순히 비교하여 큰 것을 선택하는 방법은 문제가 있다. B까지를 고려하고, 무게제한이 6인 경우. 즉 dp[2][6]에서는 기존 A와 B를 모두 담을 수 있게 되므로 최대가치가 7이 된다.
그렇다고 "그러면 i-1번째까지의 무게+i번째의 무게보다 무게제한이 커지면 가치를 더해주면 되겠구나!" 라고 단순하게 생각할 수도 없다. 배낭이 반드시 모든 물건을 담을 수 있게끔 넉넉하게 최대 무게를 설정해줄리가 없기 때문이다.
그러면 여기서 점화식을 활용해주면 된다.
i번째 물건까지 고려했을때 가방의 최대 가치 = Max{(i번째 물건이 들어가는경우, i번째 물건이 안들어가는 경우)}
이 때 i번째 물건이 들어가기 위해서는, 당연하게도 i번째 물건만큼의 무게를 추가로 필요로 한다. 따라서
max(v[i] + dp[i-1][j - w[i]], dp[i-1][j])라는 코드가 나오는것이다.
- v[i] = i번째 물건의 가치
- dp[i-1][j-w[i]] = i-1번째 물건까지 고려했을 때의 가치. 단, i번째 물건이 들어가야 하므로 w[i](i번째 물건의 무게)를 빼주어야 한다.
- dp[i-1][j] = i-1번째 물건까지 고려했을 때의 가치.
if(가방이 차있고, 물건 i가 가방에 들어갈 수 있을 때)
//물건 i를 넣는 경우와 넣지 않는 경우를 비교하여 큰 경우를 택한다.
dp[i][j] = Math.max(v[i] + dp[i-1][j - w[i]], dp[i-1][j]);
BOJ 12865) 전체 코드
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int N = sc.nextInt(); //N개의 물건
int K = sc.nextInt(); //가능한 최대 무게
int[] w = new int[N+1]; //weight
int[] v = new int[N+1]; //value
int[][] dp = new int[N+1][K+1];
int max = 0;
for(int i = 1; i <= N; i++) {
w[i] = sc.nextInt();
v[i] = sc.nextInt();
}
for(int i = 1; i <= N; i++) { //i번째 물건까지 고려
for(int j = 1; j <= K; j++) { //가능한 최대무게가 j일때
if(j >= w[i])
dp[i][j] = Math.max(v[i] + dp[i-1][j - w[i]], dp[i-1][j]); //이번물건 넣는경우 + 안넣는경우
else
dp[i][j] = dp[i-1][j];
max = Math.max(dp[i][j], max);
}
}
System.out.println(max);
}
}
'[ CS기초 ] > 알고리즘' 카테고리의 다른 글
| [알고리즘] 플로이드 알고리즘 (0) | 2023.01.09 |
|---|---|
| [알고리즘] Dijkstra (0) | 2022.09.14 |
| [알고리즘] LCS (최장 공통 부분수열) (0) | 2022.07.31 |
| [알고리즘] 유클리드 호제법 (0) | 2022.06.24 |
| [Algorithm] DFS와 BFS (with stack/queue) (0) | 2022.02.06 |