LCS(Longest Common Subsequence, 최장 공통 부분수열)
최장 공통 부분수열이란, 존재하는 두 문자열 사이에 공통으로 존재하는 부분수열 중에 가장 길이가 긴 부분수열을 의미한다. 즉, ACAYKP와 CAPCAK라는 두 문자열이 존재한다면, ACAK(ACAYKP, CAPCAK)가 두 문자열의 LCS가 된다. 부분수열이기 때문에 수열이 연속될 필요는 없다. 수열이 반드시 연속된 문자여야 할 경우 최장 공통 문자열(LCS, Longest Common Substring)이라고 한다.
LCS의 풀이는, 먼저 비교 문자열들의 길이에 따라 2차원 배열을 생성한다. 문자열 A("ACAYKP")와 문자열 B("CAPCAK")를 비교하는 상황이라고 하자. LCS[i][j]의 값은 문자열 A의 i번째 문자와 문자열 B의 j번째 문자까지 비교했을 때의 LCS값을 의미한다.
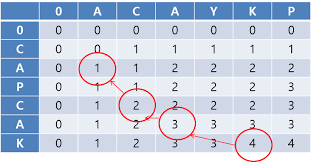
인덱스 0은 기본적으로 마진으로 사용한다. 그 다음 반복문을 이용하여 두 문자열을 비교하는데,
1. 문자열 A의 i번째 문자와 문자열 B의 j번째 문자가 다르다면, LCS[i][j]에 LCS[i-1][j]와 LCS[i][j-1] 중에 큰 값을 넣는다.
2. 위의 두 문자가 같다면, LCS[i][j]에 LCS[i-1][j-1]+1값을 넣는다.
이 두 과정을 반복하면 된다.
1번 과정은 현재 비교 인덱스의 문자가 달라도, 부분 수열이기 때문에 직전까지 진행된 최장 부분수열의 길이(LCS)는 유지된다는 것을 의미한다. 예를 들어 ACAYKP와 CAPCAK를 비교할 때, LCS[3][3]은 ACA, CAP까지 비교했을 때 LCS값이다. 이때 ACAYKP의 3번째 문자(A)는 CAPCAK의 3번째 문자(B)와 다르다. 따라서 LCS[i][j-1](=ACA, CA의 LCS값)과 LCS[i-1][j](=AC, CAP의 LCS값)중에 큰 값을 그대로 갖고오는 것이다.
2번 과정은 두 문자열이 같은 문자를 가지기 때문에, LCS값이 i와 j를 비교하기 전까지의 LCS값보다 1만큼 증가되었다는 것을 의미한다. 그래서 i와 j를 비교하는 과정 전까지의 LCS값에 1을 더해주는 것이다.
+ 추가로 LCS를 이루는 문자열을 찾으라고 할 때는, 맨 오른쪽 아래부터 LCS값이 같은 인덱스로 탐색해나가되, LCS값이 같은 인덱스가 없다면 LCS[i-1][j-1]로 이동하고 해당 인덱스를 구성하는 문자를 결과에 추가해주는 과정을 반복하면 된다.
예시) BOJ 9251: LCS (https://www.acmicpc.net/problem/9251)
import java.io.*;
import java.util.*;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
char[] str1 = br.readLine().toCharArray();
char[] str2 = br.readLine().toCharArray();
int[][] lcs = new int[str1.length+1][str2.length+1];
for(int i=0; i<=str1.length; i++)
lcs[i][0] = 0;
for(int i=0; i<=str2.length; i++)
lcs[0][i] = 0;
for(int i=1; i<=str1.length; i++) {
for(int j=1; j<=str2.length; j++) {
if(str1[i-1]==str2[j-1]) {
lcs[i][j] = lcs[i-1][j-1]+1;
}
else {
lcs[i][j] = Math.max(lcs[i][j-1], lcs[i-1][j]);
}
}
}
System.out.println(lcs[str1.length][str2.length]);
}
}'[ CS기초 ] > 알고리즘' 카테고리의 다른 글
| [알고리즘] Dijkstra (0) | 2022.09.14 |
|---|---|
| [알고리즘] 0-1 knapsack (0) | 2022.09.12 |
| [알고리즘] 유클리드 호제법 (0) | 2022.06.24 |
| [Algorithm] DFS와 BFS (with stack/queue) (0) | 2022.02.06 |
| [알고리즘] Greedy Algorithm (0) | 2022.01.15 |

