유니온 파인드 알고리즘
유니온 파인드 알고리즘은 그래프상에서 두 노드가 같은 그래프에 속하는지 판별하는 알고리즘이다.

다음과 같이 노드들이 존재할 경우, 유니온 파인드 알고리즘을 위해서는 노드를 나타내는 일차원 정수배열을 이용한다. 이 배열의 값은 노드가 속한 그래프의 정보이자, 대표 노드의 정보를 나타낸다.
당연히 배열의 초기값은 자기 자신으로 세팅한다. 연결된 노드가 없을 경우 자기 자신이 부모노드가 되기 때문이다.
초기화
처음에는 노드들 사이에 관계가 존재하지 않으므로 모든 노드는 자기 자신의 인덱스를 값으로 갖도록 초기화해준다.
int[] parent = {1,2,3,4,5,6,7,8};
Union

두 노드가 같은 그룹에 속하도록 합쳐주는 함수이다. 가장 먼저 생각할 수 있는 방법은 한 노드의 값을 다른 노드의 값으로 바꿔주면 된다. (방향성 그래프일 경우 대소비교를 통해 규칙을 커스텀 가능하다.)
void union(int a, int b) {
parent[b] = a;
}
int[] arr = {1,1,3,4,5,6,7,8}; // 편증문제 발생
그런데 이렇게만 하면 모든 노드가 자식(부모)노드를 하나씩만 가지는 편중문제가 발생할 수 있다. 그러면 트리의 depth가 깊어져서 탐색시간이 길어지고 비효율적인 트리(logn이 아니라 n에 가까운 시간복잡도)가 될 수 있다. 따라서 이를 방지하기 위해서 합치는 연산을 할 때 부모노드가 아니라, 부모노드의 대표노드를 찾아서 그 둘을 연결해주면 된다.
//a번 노드와 b번 노드를 union
//-> a집합의 대표노드를 b집합의 대표노드로 설정
void union(int a, int b) {
parent[find(b)] = find(a);
}
Find
Union 단계에서 배열의 값을 바꾸고 나서, 자신이 속한 집합의 정보를 알기 위해서는 (=자신이 속한 집합의 대표 노드를 찾기 위해서는) 다음과 같은 과정을 거친다.
예를 들어, 2번 노드가 어떤 그룹에 속하는지(=2번 노드의 대표 노드가 무엇인지)를 알기 위해서는 다음과 같이 반복문을 이용하면 된다.
1. 배열의 2번 값을 확인한다 -> 1번 (parent[2] == 1)
2. 배열의 1번 값을 확인한다 -> 1번 (parent[1] == 1)
3. 그러면 2번 노드가 속한 트리의 대표 노드는 1이다.
따라서 노드의 루트 노드를 비교해서 서로 다르면 두 노드는 다른 그래프에 속한 것이고, 같다면 동일한 그래프에 속한 것임을 알 수 있다.
그런데 이렇게 마무리할 경우 반복문을 통해서 확인하고 나오는 과정에 불필요한 반복이 들어간다. 따라서 재귀를 이용하여 n번 노드의 대표 노드 m을 찾았을 때, 대표 노드로부터 재귀를 빠져나오면서 거치는 모든 노드값의 대표 노드를 m으로 바꾸어주면 수행 시간을 줄일 수 있다.
//a번 노드가 속한 집합 정보(대표 노드) 찾기
int find(int a) {
if(a==parent[a]) return a; //대표 노드라면 그대로 반환
else return parent[a] = find(parent[a]); //대표 노드가 아니라면 부모노드에 대해 재귀탐색, 반환값을 현재 노드(a)의 대표노드로 세팅
}
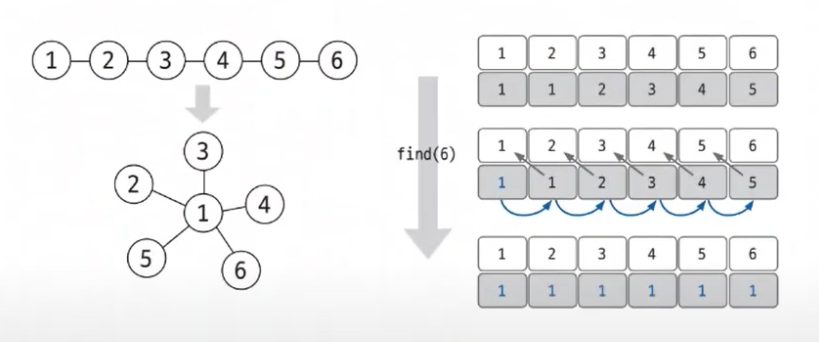
find(6)을 통해서 재귀를 빠져나오면서 모든 대표 노드들을 갱신해준다. 다시 말하면 find()연산은 자신의 대표노드를 찾을 뿐만 아니라, 그래프를 정돈하고 시간복잡도를 향상시킨다.
int find(int a) {
if(a==parent[a]) return a;
else return find(parent[a]);
}
find()함수를 이렇게 작성하면 어떻게 될까? 모든 노드값의 대표 노드값을 바꾸는 과정이 생략되어 수행시간이 늘어나게 된다.
그런데 재귀가 아니라 while문으로 구현하면 안될까? 신기하게도 while문보다 재귀를 이용한 풀이의 속도가 훨씬 빠르므로 반드시 재귀로 풀도록 하자.
대표 노드 배열이 무조건 그룹 정보를 담고있지는 않다
(BOJ17352를 풀다가 안 사실이다)
무슨 말이냐면, 그래프에서 간선의 정보가 나와있을때 union 연산을 통해서 그래프를 묶었다고 하자. 이 문제를 풀기 전 나는 대표 노드 배열에 group 정보가 담길 것이라고 생각했다.

private static void union(int a, int b) {
if(a<b) {
parent[find(b)] = find(a);
} else {
parent[find(a)] = find(b);
}
}
private static int find(int a) {
if(parent[a]==a) {
return a;
} else {
return parent[a] = find(parent[a]);
}
}
예를 들어 그림과 같은 그래프가 있을 때, 위와 같은 union, find함수를 사용해서 그래프 연결정보를 받아서 union함수를 통해 대표노드 정보를 정렬했다고 하자. 이때 대표노드를 저장한 parent배열만 보아서는 같은 그룹인지 아닌지를 판별할 수 없다.
| 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | 1 | 1 | 4 | 4 | 4 |
무조건 위와 같이 parent배열에 저장되지는 않는다는 말이다. i와 j가 같은 그룹에 있는지 판별하기 위해서는 parent[i]와 parent[j]를 비교하는 것이 아니라, find(i)와 find(j)를 비교해야 한다.
BOJ 1043) 거짓말
문제의 시간제한이 널널하기에 그냥 반복문으로 풀어도 되지만, union-find를 사용하여 다음과 같이 풀 수도 있다.
import java.io.*;
import java.util.*;
public class Main
{
static int N, M, T;
static int[] parent; //각 사람별 속한 집합을 표시
static int[] truePerson; //진실을 아는 사람들의 번호
static ArrayList<Integer>[] party; //각 파티별로 올 사람을 리스트로 저장
static int result = 0;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
String[] line_1 = br.readLine().split(" ");
N = Integer.parseInt(line_1[0]); //사람의 수
M = Integer.parseInt(line_1[1]); //파티의 개수
String[] line_2 = br.readLine().split(" ");
T = Integer.parseInt(line_2[0]);
//truePerson 배열에 진실을 아는 사람들의 번호를 저장
truePerson = new int[T];
for(int i=0; i<T; i++) {
truePerson[i] = Integer.parseInt(line_2[i+1]);
}
//각 파티에 오는 사람들의 목록을 리스트로 저장
party = new ArrayList[M];
for(int i=0; i<M; i++) {
String[] line_M = br.readLine().split(" ");
party[i] = new ArrayList<Integer>();
int party_size = Integer.parseInt(line_M[0]);
for(int j=0; j<party_size; j++) {
party[i].add(Integer.parseInt(line_M[j+1])); //파티에 오는 사람들 추가
}
}
//i가 꼭 0부터 반복되어야하나?
//parent 초기화
parent = new int[N+1];
for(int i=0; i<=N; i++) {
parent[i] = i;
}
//party에 속한 사람들이 같은 집합에 속하도록 설정
//(파티의 기준을 처음 사람으로 하여, 두번째~마지막 사람 모두를 처음 사람과 동일한 파티에 속하도록 설정한다.)
for(int i=0; i<M; i++) {
int firstPerson = party[i].get(0);
for(int j=1; j<party[i].size(); j++) {
union(firstPerson, party[i].get(j));
}
}
//각 파티별로 거짓말을 할 수 있는지 검사
for(int i=0; i<M; i++) {
boolean isPossible = true;
int cur = party[i].get(0);
//파티마다
for(int j=0; j<truePerson.length; j++) {
//만약 진실을 아는 사람중 한명과 첫번째 사람이 같은 집합에 있다면,
if(checkSame(cur, truePerson[j])) {
isPossible = false; //해당 파티에서는 거짓말을 할 수 없다.
break;
}
}
if(isPossible) result++;
}
System.out.println(result);
}
//a와 b를 같은 집합으로 설정
private static void union(int a, int b) {
a = find(a);
b = find(b);
if(a!=b) parent[b] = a;
}
//a가 속한 집합 찾기
private static int find(int a) {
if(a==parent[a]) return a;
else return parent[a] = find(parent[a]);
}
//a와 b가 같은 집합에 속하는지 검사
private static boolean checkSame(int a, int b) {
a = find(a);
b = find(b);
if(a==b) return true;
else return false;
}
}
- 초기설정:
각 사람별로 속한 집합을 나타낼 일차원 배열(parent), 진실을 알고 있는 사람들의 번호를 저장할 일차원 배열(truePerson)과 파티별로 올 사람을 리스트로 저장할 이차원 배열(party)를 이용했다. 이 때 party배열의 경우 각 파티별로 사람의 수가 상이하므로 ArrayList<Integer>형 1차원 배열으로 대체하였다.
- 사용한 함수:
- union
//a와 b를 같은 집합으로 설정
private static void union(int a, int b) {
a = find(a);
b = find(b);
if(a!=b) parent[b] = a;
}
b를 a와 같은 집합으로 세팅하는 union함수이다. 해당 문제에서는 party의 첫번째 사람을 기준으로 하여 파티에 참여한 나머지 사람들을 같은 집합으로 설정하였다.
- find
//a가 속한 집합 찾기
private static int find(int a) {
if(a==parent[a]) return a;
else return parent[a] = find(parent[a]);
}
a의 집합을 찾는 find함수이다. 재귀호출을 사용하여 a가 속한 집합(= a가 속한 파티 = a가 속한 파티의 첫번째 사람의 party[]값)을 찾아서 반환한다.
- 로직 정리:
//각 파티별로 거짓말을 할 수 있는지 검사
for(int i=0; i<M; i++) {
boolean isPossible = true;
int cur = party[i].get(0);
//파티마다
for(int j=0; j<truePerson.length; j++) {
//만약 진실을 아는 사람중 한명과 첫번째 사람이 같은 집합에 있다면,
if(checkSame(cur, truePerson[j])) {
isPossible = false; //해당 파티에서는 거짓말을 할 수 없다.
break;
}
}
if(isPossible) result++;
}
System.out.println(result);문제를 풀기 위해서 각 파티를 순회탐색하며 "파티에 속한 사람들 중 한명이라도 진실을 아는 사람과 같은 집합에 있다면" 해당 파티는 거짓말을 할 수 없는 파티로 규정하였다.
반복문만을 사용하여 문제를 풀기 위해서는 "원래는 진실을 알지 못했지만 진실을 아는 사람과 같은 파티에 속하여 진실을 알게 된 사람"의 경우를 고려해주어야 했다.
while(flag) {
flag = false;
//리스트가 true인데 리스트 내의 사람은 false인 경우
for(int i=0; i<M; i++) {
if(isPartyTrue[i]) {
for(int j=0; j<list[i].size(); j++) {
if(!isKnowing[list[i].get(j)]) {
isKnowing[list[i].get(j)] = true;
flag = true;
}
}
}
}
//리스트 내의 사람은 true인데 리스트가 false인 경우
for(int i=0; i<M; i++) {
for(int j=0; j<list[i].size(); j++) {
if(isKnowing[list[i].get(j)] && !isPartyTrue[i]) {
isPartyTrue[i] = true;
flag = true;
}
}
}
}
따라서 반복문을 사용했던 방법인 위 코드는 while문으로 이중 반복문을 감싸서 첫번째 케이스인 "해당 파티는 진실을 아는 파티인데, 그 파티 내의 사람이 진실을 모른다고 되어있어서 그 사람을 진실을 안다고 설정해주어야 하는 경우"와 두번째 케이스인 "해당 파티는 진실을 알지 못하는 파티인데, 그 파티 내의 사람이 진실을 알아서 해당 파티 내의 사람들을 모두 진실을 안다고 설정해주어야 하는 경우"를 계속 검사하여 그러한 케이스가 나오지 않을 때까지 반복해주어야 했다.
하지만 union-find를 사용할 경우, 파티에 참여하는 모든 사람들이 union함수를 통하여 집합으로 묶여있기 때문에, find함수를 사용하여 "진실을 아는 사람이 파티에 속해있는지" 여부만 검사해주면 된다.
'[ CS기초 ] > 알고리즘' 카테고리의 다른 글
| [알고리즘] Traveling Salesman Problem (0) | 2024.04.08 |
|---|---|
| [알고리즘] LIS로 알아보는 역추적 기법 (0) | 2024.03.23 |
| [알고리즘] 누적합(부분 배열 합) (0) | 2023.02.18 |
| [알고리즘] 플로이드 알고리즘 (0) | 2023.01.09 |
| [알고리즘] Dijkstra (0) | 2022.09.14 |

